一、初步尝试画圆角矩形

要在Canvas中绘制一个矩形，使用strokeRect或fillRect函数即可。

var canvas = document.getElementById("canvas");
var ctx = canvas.getContext("2d");

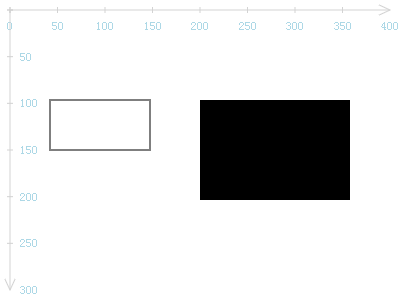
ctx.strokeRect(50, 100, 100, 50);
ctx.fillRect(200, 100, 150, 100);

将得到下面的图形：

实现方法一：设置lineJoin属性设置为round（推荐指数：*）

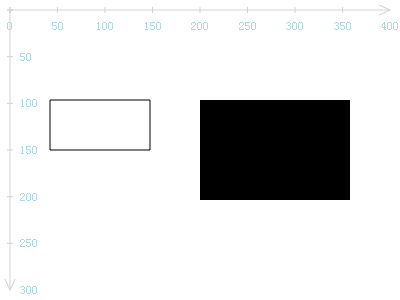
要想绘制出圆角矩形，好办，将ctx的lineJoin属性设置为round即可。

ctx.lineJoin = "round";
ctx.strokeRect(50, 100, 100, 50);
ctx.fillRect(200, 100, 150, 100);

这是圆角矩形吗？没错，只不过角度太小了。将ctx的lineWidth属性增大一些，效果就出来了。

ctx.lineJoin = "round";
ctx.lineWidth = 20;

ctx.strokeRect(50, 100, 100, 50);
ctx.fillRect(200, 100, 150, 100);

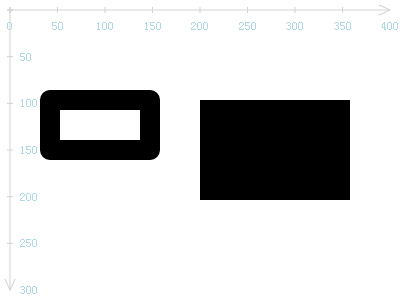
左边的圆角效果出来了，但代价是必须指定线条宽度，以让ctx有空间来填充该线条，才能有圆角效果。若想要更大的圆角，虽可增加lineWidth，但将得到更大的黑框，更丑了。而右边的填充图形，却根本没有圆角效果出现。

这不是我们所想要的效果，所以不推荐该方法。

二、圆角矩形的真谛

我们，想要的是下面这个效果：

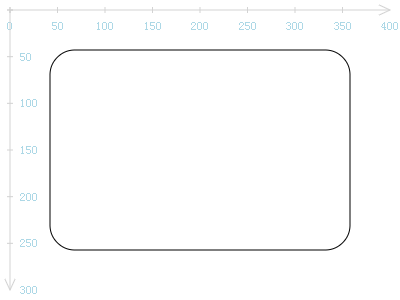
经验告诉我们，这个矩形的圆角可大可小。那么这些圆角有何内在规律呢？下图可说明。

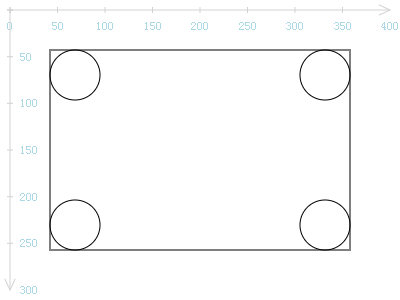
矩形的4个角均各自夹着一个与该角之两边相切的圆，将矩形的4个棱角擦掉，只保留两个相切点之间的较短的圆弧，即可得到上面的圆角矩形。

这4个圆的半径均是25。若将半径改为40，得到下图。

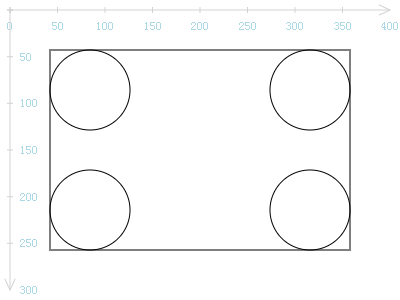
矩形的总体特征不变，但圆角增大了。当然，圆角太大了也不一定好看，但上面这两个图形足以说明了圆角矩形的真谛。要想改变矩形圆角的大小，只需改变这些相切圆的半径就行了。

三、圆角矩形的实现

一个标准矩形与4个相应的圆的关系，这是我们要实现圆角矩形所需考虑的。可以有多种实现方法，既可通过圆形异或的方式，也可通过裁剪的方式，但最直观的方式莫过于通过勾画圆角矩形的外边框来实现了，即，画直线，画圆弧，再画直线，再画圆弧……直至任务完成。

直线好画，关键是画圆弧。Canvas提供了两个画圆弧的函数，arc及arcTo，下面分别考察。

实现方法二：以arc实现圆角效果及逐步分析（推荐指数：****）

arc的原型如下：

arc(x, y, r, startAngle, endAngle, isCounterClocksise)

参数x, y确定圆心位置，r确定半径大小。startAngle为起始角度，endAngle为终止角度。角度的起算方向为下图。

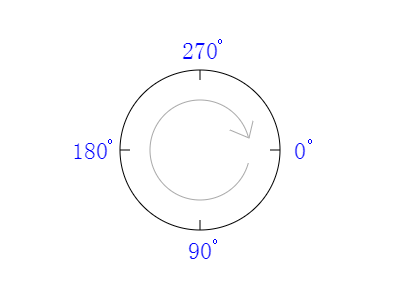
水平方向的右侧为0o，依顺时针方向逐渐增大角度，转至0o位置时为360o。

arc函数中的startAngle及endAngle均采用弧度制，这与我们日常生活中采用的角度制不同。弧度、角度的互换公式如下：

radian = π / 180 * degree = Math.PI / 180 * degree
degree = 180 / π * radian = 180 / Math.PI * radian

因此，60o换算为弧度制的公式是：

var angle = Math.PI / 180 * 60;

因为可以指定startAngle及endAngle， 因此可以绘制一条非完整圆的弧线。而给定起始角与终止角，只要这两个角度不是相差180o，依不同的绘制方向，将得到长弧或短弧两条弧线。下图说明了此问题。

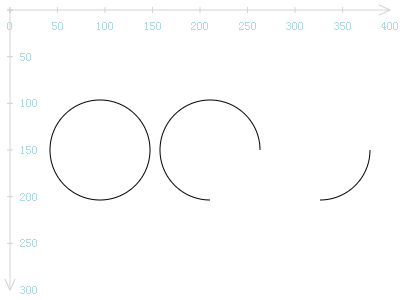
左边的圆的绘制函数为：

ctx.arc(100, 150, 50, 0, Math.PI * 2, true);

因为起始角为0o，终止角为360o，正好形成一个完整的圆圈。此时arc的最后一个参数isCounterClockwise为true或为false均无所谓。

中间的圆弧的绘制函数为：

ctx.arc(210, 150, 50, 0, Math.PI / 180 * 90, true);

从0o绘至90o，由于参数isCounterClockwise为true，要求按逆时针方向来绘制，因此绘制了一个从0o逆时针行至90o的长弧。

右边的圆弧的绘制函数起始角与终止角与上例相同，只是绘制方向依顺时针方向：

ctx.arc(320, 150, 50, 0, Math.PI / 180 * 90, false);

从0o顺时针行至90o，得到一条短弧。

了解了arc的用法，现在可以用它来实现圆角矩形了。下图重复展现我们的目标。

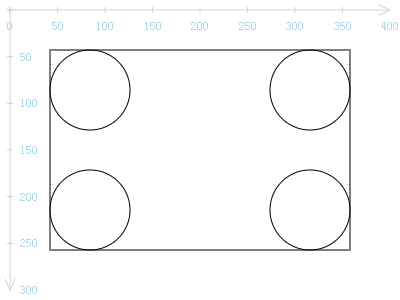
对于4个相切的圆圈，给定矩形的左上角顶点与该矩形的宽度与高度，其圆心与半径均不难求出。

以arc实现圆角具体代码

我们先从左上角相切的顶边切点开始，画一直线至右上角相切的顶边切点，然后绘制一条270o顺时针至0o的短圆弧。之后，直线，0o顺时针至90o的短圆弧，直线，90o顺时针至180o的短圆弧，直线，180o顺时针至270o的短圆弧。任务完成。代码如下：

function Rect(x, y, w, h) {
    return {x:x, y:y, width:w, height:h};
}

var rect = Rect(50, 50, 300, 200);
var r = 40;

drawUsingArc(rect, r, ctx);

function drawUsingArc(rect, r, ctx) {
    var path = new Path2D();

    path.moveTo(rect.x + r, rect.y);
    path.lineTo(rect.x + rect.width - r, rect.y);
    path.arc(rect.x + rect.width - r, rect.y + r, r, Math.PI / 180 * 270, 0, false);
    path.lineTo(rect.x + rect.width, rect.y + rect.height - r);
    path.arc(rect.x + rect.width - r, rect.y + rect.height - r, r, 0, Math.PI / 180 * 90, 0, false);
    path.lineTo(rect.x + r, rect.y + rect.height);
    path.arc(rect.x + r, rect.y + rect.height - r, r, Math.PI / 180 * 90, Math.PI / 180 * 180, false);
    path.lineTo(rect.x, rect.y + r);
    path.arc(rect.x + r, rect.y + r, r, Math.PI / 180 * 180, Math.PI / 180 * 270, false);

    ctx.stroke(path);
}

Rect是一个无需使用new来创建一个新对象的构造函数。它将一个矩形所需的数据打包进其自身中，并可在以后通过特定的属性来方便地访问相应的数据。对于Point、Line、Rect这种简单的数据包装结构，使用这种方式使代码更加简洁。

函数drawUsingArc的参数中可指定矩形及其圆角半径，这样函数的意义就变成了绘制一个半径为r的圆角矩形。

总结：该方法可以灵活实现圆角矩形，但是需要多次使用lineTo和arc接口画线和画圆。操作步骤较多，性能稍差。

实现方法三：以arcTo实现圆角效果（推荐指数：*****）

如同lineTo的意义为”画线至…”, arcTo的意义为”画圆弧至…”。arcTo的原型如下：

arcTo(x1, y1, x2, y2, r)

参数中需传入2个点的坐标值，以及一个半径值。虽然同为画圆弧，但arcTo与arc的原型大相径庭，令人百思不得其解。不要紧，先用arcTo画出一段圆弧来看看。

ctx.moveTo(100, 200);
ctx.lineTo(200, 200);
ctx.arcTo(260, 260, 300, 100, 20);
ctx.stroke();

坐标值是随机选定的，只需要随便画出一条看得见的圆弧来就行。画出了下图效果：

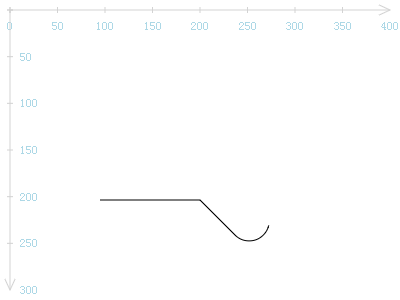
从点(100, 200)画水平线至点(200, 200)，然后调用arcTo来画圆弧。我们知道，使用lineTo()绘制直线时，将使当前点移至lineTo()参数所确定的点的位置。从图中可看出，从水平线的终点(200, 200)，也即当前点，到圆弧的起点，多出了一条直线，应是arcTo函数自动添加的，以使当前点与圆弧得以连接起来形成一个连续的图形。这也是arcTo函数之所以这样取名的原因：可别忘了，我会自动以直线连接当前点与圆弧起点。

可问题是，这段圆弧为何出现在图中这个位置？圆弧的起点好像并不在其参数两个点所确定的位置。为证明此点，先用红色标出arcTo参数中的两个点(260, 260)与(300, 100)。

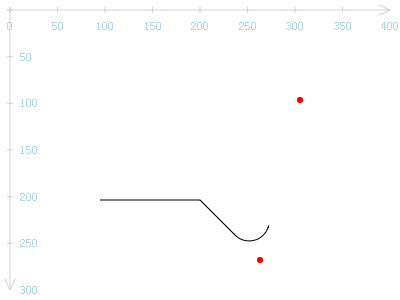
圆弧的起点与终点均不位于其参数所确定的两点上的位置。为何根据这两个似乎毫不相关的两点，就能画出图中的圆弧？

两点确定一线，何不将两红点连起来看看？

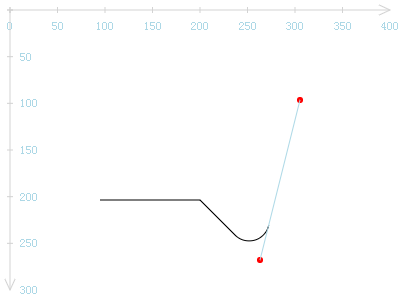
直线与圆弧相交于一点。是相交，是否相切？我们将这段圆弧延展为一个圆来看看。因为arcTo参数中已经指定了半径，以此半径为依据画一圆圈，并在平面上移动它，使该圆圈的下方与arcTo的圆弧大致重合。

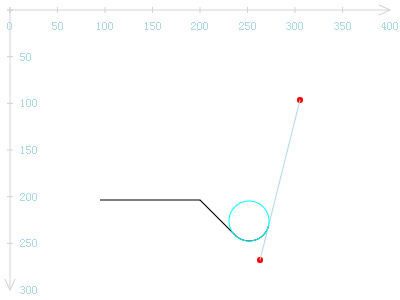
令人想不到的是，圆弧确实与这条看不见的直线相切! 这实在是我到现在为止所发现的最匪夷所思的秘密了！

球好像向右滚着掉进了一个有缺口的三角缝中。缝太大了，球会掉进万丈深渊的。因此，延长arcTo所自动添加的线段，让其直抵右边的直线。

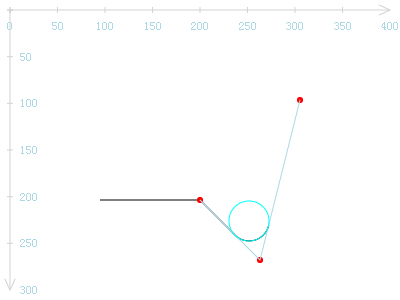
延长线与右边直线相交于点(260, 260)，也即arcTo的第一、第二个参数所确定的点。并且，延长线也相切于圆弧。

把辅助圆圈擦掉，得到下图：

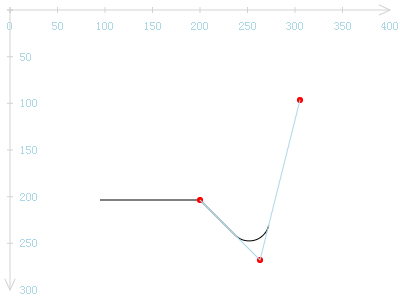
现在，真相大白了。arcTo的圆弧具备以下特点：

• 圆弧将与两条直线相切
• 第一条直线是当前点的位置与参数(x1,y1)所组成的直线
• 第二条直线是参数(x1,y1)与参数(x2,y2)所组成的直线
• 如果当前点与圆弧起点不在同一点，则从当前点绘制一条直线至圆弧起点。

简而言之，圆弧存活于这3点所构成的夹角中。

arcTo自动添加的直线有点超出人力所为，终难所料，能否去除它？将arcTo参数中的第一个点改为与当前点一样，即(200, 200)。

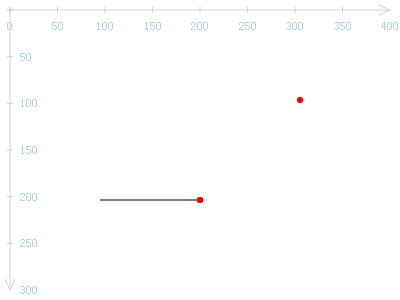
这条自动添加的直线是消失了，但圆弧也消失了。别忘了我们说过的话，圆弧存活于3点所构成的夹角中。现在既然3点变为2点，不再有夹角，圆弧也失去生存的意义了。

3点的夹角。这3点如果构成了一个直角呢？

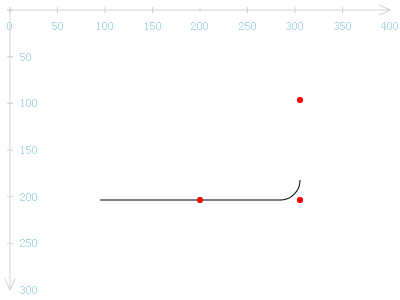
嘿，这不就是圆角矩形的一个圆角吗？因为arcTo会将当前点归置于圆弧的终点，因此，我们简单地接着使用一个lineTo()函数即可将上面的红点也连接起来，从而形成一个真正的圆角。(但如果依照规律连续调用arcTo()函数，由于其会自动连接当前点与圆弧起点的特点，lineTo()的调用也可以省去了。)

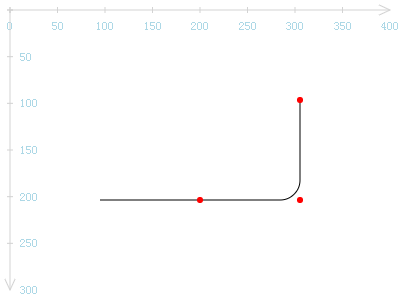
综上，可以使用arcTo来实现圆角矩形了。

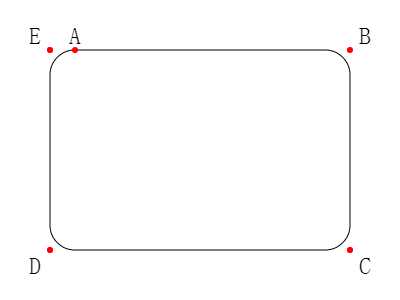
上图中，关键点用红色标出，且从点A按顺时针方向绘制。其简化的伪代码如下：

moveTo(PointA);
arcTo(PointB, PointC);
arcTo(PointC, PointD);
arcTo(PointD, PointE);
arcTo(PointE, PointA);

移至点A，朝ABC的方向在点B画圆弧，并将当前点置于点B所在圆弧的下方。朝BCD的方向在点C画圆弧，朝CDE的方向在点D画圆弧，朝DEA的方向在点E画圆弧。点E处的圆弧的终点将与点A连接起来，从而构成了一个完整的圆角矩形。一样子就用4条线（直线+弧线）组成了一个圆角矩形。

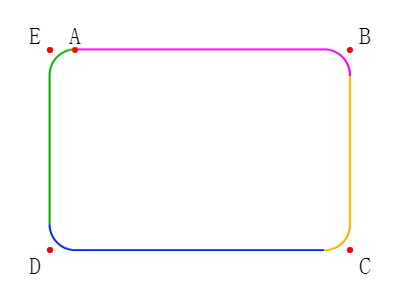
除矩形的4个角之外，还引入了一个点A。如果从点E直接绘制，则EA将产生一条线段，从而破坏了圆角。

依据上面的伪码，使用arcTo绘制圆弧的代码为：

var Point = function(x, y) {
    return {x:x, y:y};
};

var rect = Rect(50, 50, 300, 200);

drawRoundedRect(rect, 25, ctx);

function drawRoundedRect(rect, r, ctx) {
    var ptA = Point(rect.x + r, rect.y);
    var ptB = Point(rect.x + rect.width, rect.y);
    var ptC = Point(rect.x + rect.width, rect.y + rect.height);
    var ptD = Point(rect.x, rect.y + rect.height);
    var ptE = Point(rect.x, rect.y);

    ctx.beginPath();

    ctx.moveTo(ptA.x, ptA.y);
    ctx.arcTo(ptB.x, ptB.y, ptC.x, ptC.y, r);
    ctx.arcTo(ptC.x, ptC.y, ptD.x, ptD.y, r);
    ctx.arcTo(ptD.x, ptD.y, ptE.x, ptE.y, r);
    ctx.arcTo(ptE.x, ptE.y, ptA.x, ptA.y, r);

    ctx.stroke();
}

所绘圆角矩形如下：

方法四：arcTo优化版（强烈推荐）

最后仿照rect方法的语法，我们再写一个更灵活实用的圆角矩形的方法。代码如下：

// 入参说明：上下文、左上角X坐标，左上角Y坐标，宽，高，圆角的半径
function arcRect (ctx, x, y, w, h, r) { 
  // 右上角弧线
  ctx.moveTo(x + r, y);
  ctx.arcTo(x + w, y, x + w, y + r, r);

  // 右下角弧线
  ctx.moveTo(x + w, y + r);
  ctx.arcTo(x + w, y + h, x + w - r, y + h, r);

  // 左下角弧线
  ctx.moveTo(x + w - r, y + h);
  ctx.arcTo(x, y + h, x, y + h - r, r);

  // 左上角弧线
  ctx.moveTo(x, y + h - r);
  ctx.arcTo(x, y, x + r, y, r);
}